On entend partout parler de chiffres, de prévisions, de données… Mais nous n’entendons rarement parler de la méthode permettant de partir des questions pour obtenir des réponses.
C’est pourquoi je me suis essayé à un petit jeu en lien avec mon cursus. Essayé de faire des prédictions sur les chiffres du COVID-19 avec une courbe logistique.
Je l’avoue, il y a moins morbide comme prévision mais il s’agit ici plus de Mathématiques et d’informatique!
Modèle, modèle… qui est le plus beau?
Et oui! Beaucoup de méthodes existent pour faire des prédictions…
J’ai choisis de faire simple, j’ai choisis un modèle dépendant de paramètres et de trouver lesquels minimiserait « l’erreur ». Il s’agît d’une méthode dite paramétrique.
Mais quelle modèle choisir… Pour cela il faut déjà choisir quelle sera la variable à estimer.
J’ai choisis le nombre de mort total en fonction du nombre de jour. Maintenant un autre problème, quel modèle utiliser pour notre estimations?
Prenons un cas avancé de l’épidémie de COVID-19, nous allons donc étudier la courbe de la France et la comparer avec une courbe logistique.

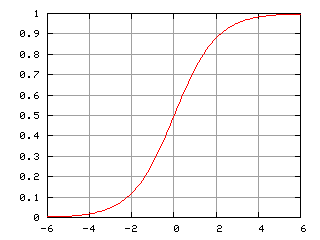
Il y a un petit air de famille… Non?
La question est donc quel courbe logistique correspond le mieux à notre courbe à droite? Et oui, il y en a plusieurs!
En voici quelque une:
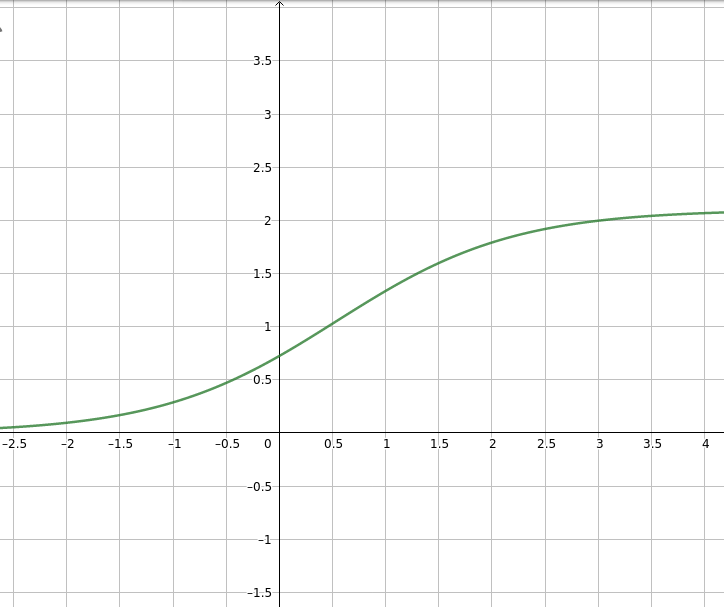
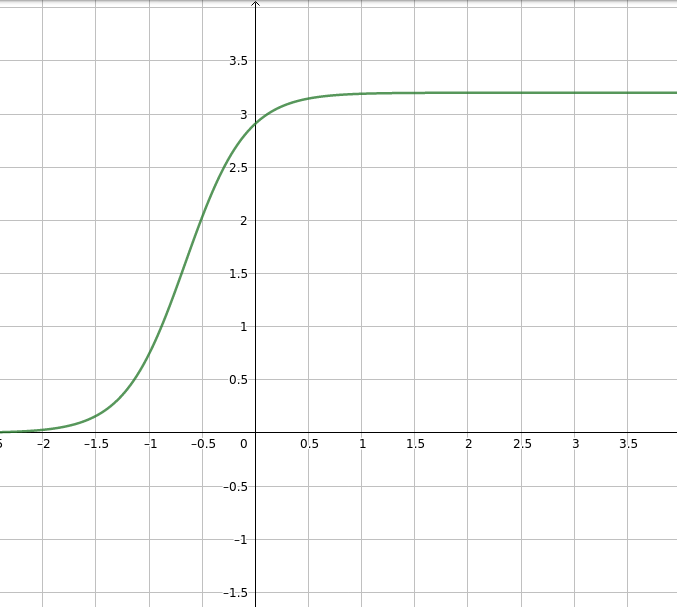
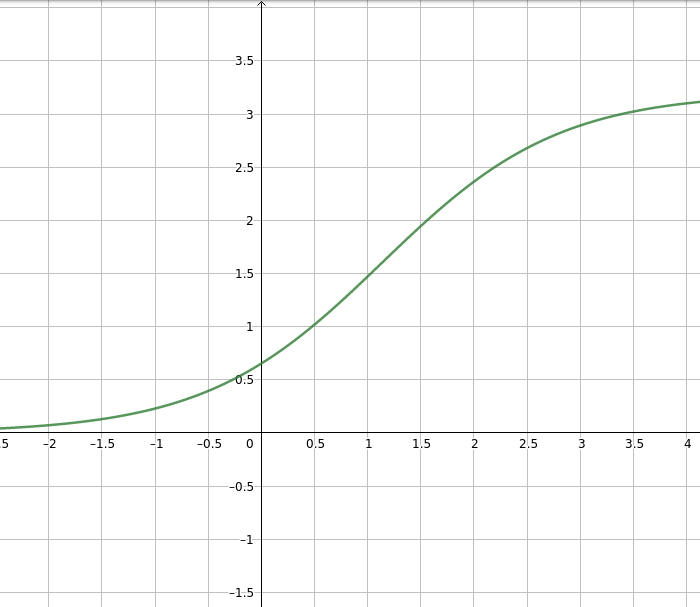
Je pense donc que ce sera notre modèle
Comment trouver la bonne courbe logistique ?
Je vous ai présenté donc un modèle. Ce modèle nous donne un ensemble de courbe qui peuvent être construites à partir de trois paramètres: largeur, hauteur et décalage.
Il faut donc trouvé ces trois paramètres qui minimise « l’erreur ».
Mais qu’est ce que l’erreur? Comment minimiser?
Il faut définir l’erreur!
Et là, nous avons plusieurs possibilités mais fixons en premier un cadre théorique. L’erreur est une fonction qui dépend de nos trois paramètres. Elle permet de savoir si la courbe est « loin » de notre courbe pratique. L’erreur est construite à partir des points réels donc dans notre cas, les morts chaque jour.
Mais comment construire l’erreur me demanderiez vous? Plusieurs réponses sont possible mais je ne pense pas avoir des connaissances suffisantes pour expliquer laquelle choisir et pourquoi. Donc je vais construire l’erreur par la méthode dite des « moindres carrés ». Cette méthode consiste simplement à donner la distance des points construits par notre modèle aux points réels.
Une petite illustration sur le COVID-19
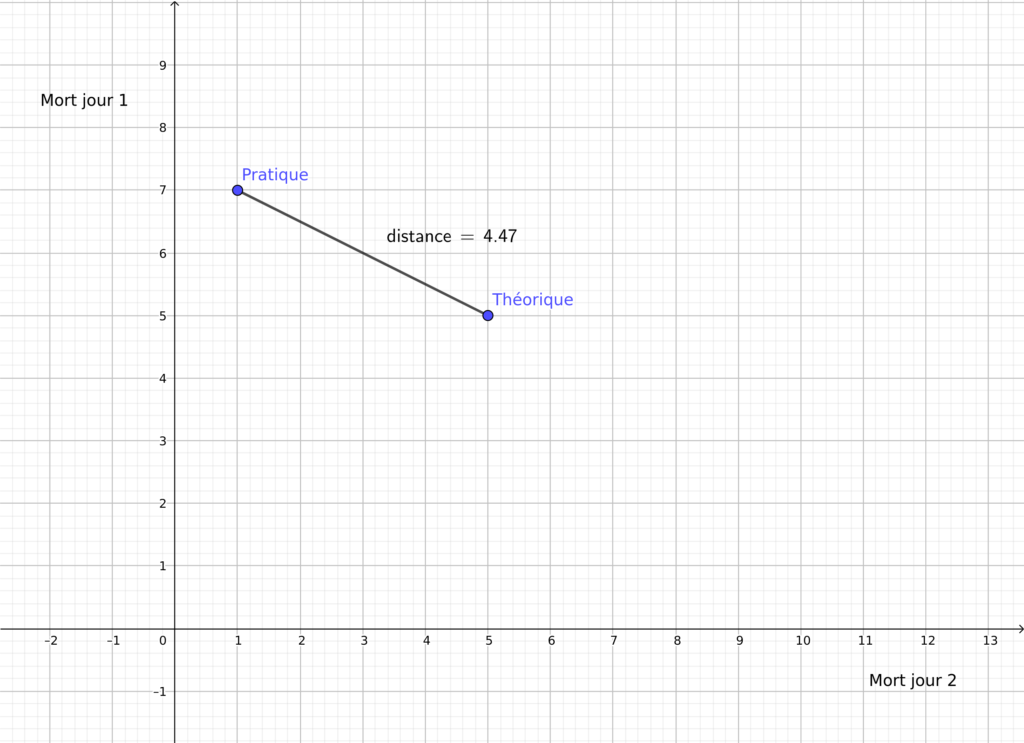
Nous voyons bien ici que pour deux jour, nous avons deux dimensions (deux axes) et deux points : un point pratique et un point théorique.
Chaque point est positionné devant le nombre de mort jour 1 et jour 2. On remarque que le nombre de mort pratique le premier jour est de 7 alors que le deuxième jour, il y a 1 mort.
Il faut maintenant bien comprendre que si l’on peut faire le même raisonnement sur trois jours alors le graphique sera en 3D donc pour quatre jours, le graphique sera en 4D etc… Il reste bien sur difficile de visualiser plus de 3 dimension mais il est possible d’effectuer les calculs mathématiquement en plus grande dimension.
Donc l’erreur à minimiser est la distance entre ses deux points mais l’on ne peux pas rapprocher aussi facilement les points! Déjà le point théorique est fixe et dépend du nombre de mort annoncé chaque jour et le point pratique qui est calculé à partir de la fameuse courbe logistique dépendant des trois paramètres. Nous parlerons de comment trouver ces trois paramètres dans un article sur la descente de gradient !
Vous pouvez essayer de vous faire une idée de comment approcher les deux points avec ce petit programme :
https://www.geogebra.org/calculator/vpsry2cz
Après le choix du modèle… l’optimisation!
Nous n’allons pas rentrer dans les détails techniques de l’optimisation du modèle par le critère des moindres carrés (la distance vu précédemment). Mais nous allons voir les résultat de celui ci!
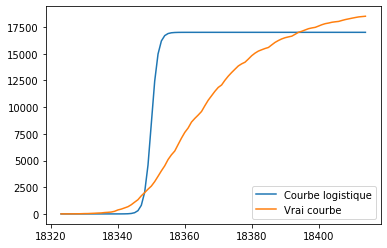

Nous voyons ici la courbe logistique avant et après l’optimisation. Elle s’est rapproché la courbe logistique réelle des morts dû au COVID-19. Elle n’est pas parfaitement dessus mais il s’agit d’un comportement normal puisque qu’aucune courbe logistique n’est exactement égale à la vrai courbe!
Maintenance, nous pouvons donc prédire le jour suivant à partir des jours précédents !
Toutes mes prédictions!
Nous allons donc voir ici toutes mes prédictions faites durant le confinement ! L’erreur moyenne pourra donc être calculé avec les prédictions.

Ici un petit problème se pose devant nous, les prédictions ont tendances à s’éloigner de la vrai courbe… L’erreur moyenne est donc : 438 ! Ce qui est très élevé!
Ce qui est normal puisque la courbe logistique n’est pas le modèle exacte ! Il faudrait prendre un modèle plus fin donc avec plus de paramètres pour obtenir de meilleurs résultats. Peut-être une prochaine fois!

